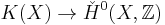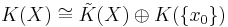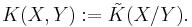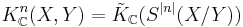Topological K-theory

In mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as (general) K-theory that were introduced by Alexander Grothendieck. The early work on topological K-theory is due to Michael Atiyah and Friedrich Hirzebruch.

1 Definitions
2 Properties
3 Bott periodicity
4 See also
5 References

Definitions

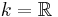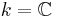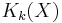Let X be a compact Hausdorff space and $k=\mathbb{R}$ or $k=\mathbb{C}$ . Then $K_{k}(X)$ is the Grothendieck group of the commutative monoid whose elements are the isomorphism classes of finite dimensional $k$ -vector bundles on X with the operation

$[E]\oplus [F] = [E\oplus F]$

for vector bundles E, F. Usually, 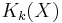$K_k(X)$ is denoted 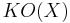$KO(X)$ in real case and 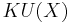$KU(X)$ in the complex case.

More explicitly, stable equivalence, the equivalence relation on bundles E and F on X of defining the same element in K(X), occurs when there is a trivial bundle G, so that

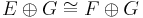$E\oplus G\cong F\oplus G$ .

Under the tensor product of vector bundles K(X) then becomes a commutative ring.

The rank of a vector bundle carries over to the K-group. Define the homomorphism

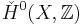$K(X)\to\check{H}^0(X,\mathbb{Z})$

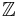where $\check{H}^0(X,\mathbb{Z})$ is the 0-group of Čech cohomology which is equal to the group of locally constant functions with values in $\mathbb{Z}$ .

If X has a distinguished basepoint x₀, then the reduced K-group (cf. reduced homology) satisfies

$K(X)\cong\tilde K(X)\oplus K(\{x_0\})$

and is defined as either the kernel of 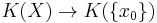$K(X)\to K(\{x_0\})$ (where 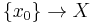$\{x_0\}\to X$ is basepoint inclusion) or the cokernel of 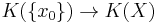$K(\{x_0\})\to K(X)$ (where 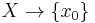$X\to\{x_0\}$ is the constant map).

When X is a connected space, 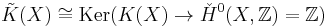$\tilde K(X)\cong\operatorname{Ker}(K(X)\to\check{H}^0(X,\mathbb{Z})=\mathbb{Z})$ .

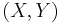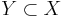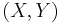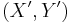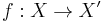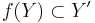The definition of the functor K extends to the category of pairs of compact spaces (in this category, an object is a pair $(X,Y)$ , where $X$ is compact and $Y\subset X$ is closed, a morphism between $(X,Y)$ and $(X',Y')$ is a continuous map $f:X\to X'$ such that $f(Y)\subset Y'$ )

$K(X,Y):=\tilde{K}(X/Y).$

The reduced K-group is given by 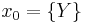$x_0=\{Y\}$ .

The definition

$K_{\mathbb{C}}^{n}(X,Y)=\tilde K_{\mathbb{C}}(S^{|n|}(X/Y))$

gives the sequence of K-groups for 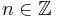$n\in\mathbb{Z}$ , where S denotes the reduced suspension.

Properties

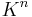$K^n$ is a contravariant functor.
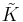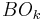The classifying space of $\tilde{K}$ is $BO_k$ (BO, in real case; BU in complex case), i.e. $\tilde{K}_k(X)\cong[X,BO_k].$
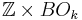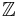The classifying space of $K$ is $\mathbb{Z}\times BO_k$ ( $\mathbb{Z}$ with discrete topology), i.e. $K_k(X)\cong[X,\mathbb{Z}\times BO_k].$
There is a natural ring homomorphism 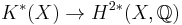$K^*(X)\to H^{2*}(X,\mathbb{Q})$ , the Chern character, such that 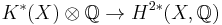$K^*(X)\otimes\mathbb{Q}\to H^{2*}(X,\mathbb{Q})$ is an isomorphism.
Topological K-theory can be generalized vastly to a functor on C*-algebras, see operator K-theory and KK-theory.

Bott periodicity

The phenomenon of periodicity named for Raoul Bott (see Bott periodicity theorem) can be formulated this way:

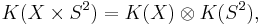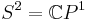$K(X\times S^2)=K(X)\otimes K(S^2),$ and $K(S^2)=\mathbb Z[H]/(H-1)^2;$ where $H$ is the class of the tautological bundle on the $S^2=\mathbb CP^1$ , i.e. the Riemann sphere as complex projective line.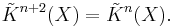
$\tilde K^{n%2B2}(X)=\tilde K^n(X).$
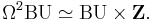
$\Omega^2\mathrm{BU}\simeq\mathrm{BU}\times\mathbf Z.$

In real K-theory there is a similar periodicity, but modulo 8.

References

M. Karoubi, K-theory, an introduction, 1978 - Berlin; New York: Springer-Verlag
M.F. Atiyah, D.W. Anderson K-Theory 1967 - New York, WA Benjamin
A. Hatcher Vector Bundles & K-Theory

Topological K-theory

Contents

Definitions

Properties

Bott periodicity

See also

References